Úvod do světa dluhopisů: Cena a výnos dluhopisu

23.11.2021 16:38

Třetí díl seriálu o dluhopisech bude pojednávat o ceně a výnosu dluhopisů. První část článku bude věnována ceně – jak můžeme cenu vnímat, jakým způsobem bývá vyjádřena a jaké faktory ji ovlivňují. Obsahem druhé části bude seznámení s výnosem z dluhopisu, především jaké typy výnosu rozlišujeme. Závěr bude pojednávat o tom, jaký je vztah mezi cenou a výnosem u dluhopisů. Představen bude také pojem durace.

Tržní vs. teoretická cena

Tržní cena dluhopisu na trhu je stejně jako u akcií dána na základě nabídky a poptávky.

U dluhopisu můžeme spočítat tzv. teoretickou cenu / hodnotu, která je rovna současné hodnotě veškerých budoucích peněžních toků plynoucích z daného dluhopisu. U bezkupónového dluhopisu se bere v potaz jediný peněžní tok z dluhopisu, a to jmenovitá hodnota, která bude vyplacena k datu splatnosti. Ta se diskontuje (vzhledem k časové hodnotě peněz přepočte na současnou hodnotu), čímž se určí aktuální teoretická cena. Teoretická cena se poté dá porovnat s cenou na trhu a vyhodnotit tak, zda je dluhopis podhodnocen či nadhodnocen. Pokud by se jednalo o kupónový dluhopis, je nutné kromě jmenovité hodnoty diskontovat všechny budoucí kupóny.

Výpočet teoretické ceny dluhopisu s třemi pevnými kupóny vyplácenými jednou ročně. Po třech letech je společně s kupónem splacena také jmenovitá hodnota. Jednotlivé budoucí kupóny (C) a jmenovitou hodnotu (JH) aktualizujeme na současnou hodnotu dělením výrazem (1+i) umocněným na příslušnou dobu do výplaty daného peněžního toku vyjádřenou v letech, i je tržní úroková míra.

Jak je na burze vyjádřena cena dluhopisu?

Čistá cena (clean price) odráží aktuální tržní cenu samotného dluhopisu (bez uvažování kupónových plateb). Může se pohybovat v závislosti na vývoji trhu (např. změny očekávání vývoje úrokových sazeb či bonity dlužníka), což může způsobovat její volatilitu.

Alikvotní úrokový výnos (AÚV) označuje část kupónu naběhlou k určitému okamžiku v období mezi výplatami kupónů. Pro každého dluhopisového investora je AÚV spravedlivý, jelikož dostane přesně tu část, na kterou má vzhledem k době držby nárok. Každým dnem, co investor dluhopis drží, jeho alikvotní úrokový výnos rovnoměrně narůstá.

Celková cena (dirty price) je druhý způsob, jakým lze na burze vyjádřit cenu dluhopisu. Jedná se o částku, kterou investor za dluhopis zaplatí celkem. Skládá se z čisté ceny a AÚV.

Jakým způsobem jsou ceny dluhopisů na různých burzách stanoveny (zda v čisté či celkové ceně), si uvedeme v jednom z dalších dílů tohoto seriálu.

Cenu dluhopisu a kalkulaci AÚV uvedeme na konkrétním příkladu. Uvažujeme dluhopis se jmenovitou hodnotou 100.000 Kč, jenž vyplácí kupón 4.000 Kč jednou ročně, vždy k datu 1.1. daného roku.

Pokud chceme určit cenu za dluhopis přesně čtvrt roku od poslední výplaty kupónu (to znamená k 1.4.), k čisté ceně dluhopisu kótované na trhu musíme přičíst naběhlou část kupónu (AÚV). Jelikož celkový roční kupón činí 4.000 Kč, za čtvrt roku naběhne přesně čtvrtina ročního kupónu, tedy 1.000 Kč.

Grafické znázornění AÚV: Kupón nabíhá rovnoměrně po celé období, čímž narůstá AÚV. V den ex-date (první den, kdy se dluhopis obchoduje bez nároku na nejbližší kupón) klesá AÚV na nulu a počátkem tohoto dne začíná opět rovnoměrně růst až do dalšího rozhodného dne. Tento proces platí pouze v případě, že je ex-date shodný s dnem vypořádání (tzv. settlement day). Pokud by den vypořádání následoval až po ex-date (např. u českých státních dluhopisů – vypořádání nastává až měsíc po ex-date), poklesne AÚV do záporných hodnot a do kladných hodnot přechází až v den, který následuje po dni vypořádání.

Jaké faktory ovlivňují cenu?

Na vývoj teoretické ceny dluhopisu působí čtyři základní faktory. Krátce jsme se o nich již zmínili v předchozím díle.

Prvním faktorem jsou tržní úrokové sazby. V případě jejich růstu tržní cena dluhopisu klesá, jelikož každý peněžní tok z dluhopisu diskontujeme vyšší úrokovou sazbou, tedy současná hodnota jednotlivých peněžních toků se snižuje. Obecně se dá také říci, že tržní ceny dluhopisů bývají méně citlivé na růst úrokových sazeb než na jejich pokles.

Na změnu úrokových sazeb však nereagují všechny dluhopisy stejně citlivě. Dostáváme se tak k druhému faktoru, který ovlivňuje hodnotu dluhopisu. Tím je doba do splatnosti. Dluhopisy s delší splatností jsou obvykle více citlivé na změnu tržních úrokových sazeb než krátkodobé dluhopisy.

Třetím faktorem je výše kupónových plateb. Dluhopisy vyplácející vyšší kupóny jsou zpravidla méně citlivé na změnu tržních úrokových sazeb než dluhopisy s nízkou či nulovou kupónovou výplatou.

Posledním faktorem, který cenu dluhopisu menší či větší měrou ovlivňuje, je jeho jmenovitá hodnota. Cena se obvykle s přibližujícím se časem splatnosti přibližuje jmenovité hodnotě, v čase splatnosti se jmenovitá hodnota a teoretická cena rovnají.

Výnos z dluhopisu

Výnos z dluhopisu chápeme jako rozdíl mezi součtem plateb obdržených z dluhopisu po dobu jeho života a pořizovací cenou. Zatímco úrokový výnos označuje sumu obdržených úrokových plateb z dluhopisu, kapitálový výnos představuje samotný rozdíl mezi pořizovací a prodejní cenou. V případě, že investor drží dluhopis do splatnosti, za prodejní cenu se považuje jmenovitá hodnota, která je vyplacena ke dni splatnosti.

Na výnosnost dluhopisu můžeme nahlížet vícero způsoby. V závislosti na typu výnosu je nezbytné výsledné číslo správně interpretovat.

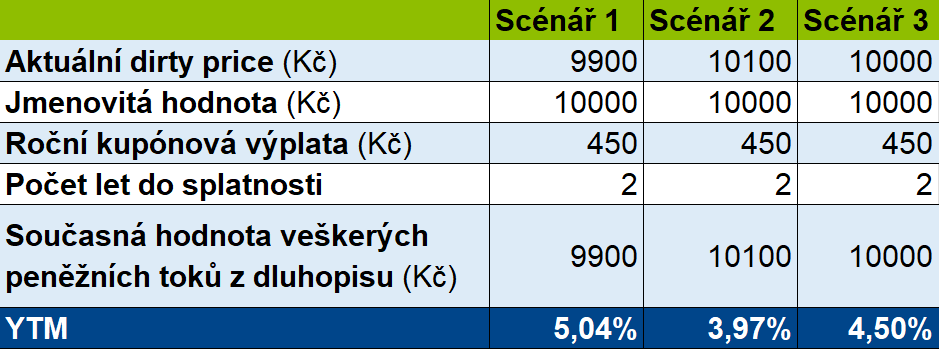
Jednotlivé výpočty si budeme ilustrovat na příkladu dluhopisu s jmenovitou hodnotou 10.000 Kč a ročním kupónem 450 Kč. Namodelujeme si dvě situace, kdy v prvním scénáři jeho cena bude činit 9.900 Kč a v druhém scénáři 10.100 Kč.

Kupónový výnos

Kupónový výnos značí, kolik procent jmenovité hodnoty investor ročně získá z kupónových výplat.

Kupónový výnos vypočteme jako podíl kupónové platby (450 Kč) a jmenovité hodnoty (10.000 Kč), čímž dostaneme výsledek 0,045, neboli 4,5 %, což je roční kupónový výnos vyplývající z držby tohoto dluhopisu. Důležité je upozornit, že při výpočtu kupónového výnosu nebereme v potaz tržní cenu, avšak jmenovitou hodnotu, která se od tržní ceny může lišit. Proto je kupónový výnos u obou scénářů totožný.

Běžný výnos

Podobným ukazatelem jako kupónový výnos je běžný výnos, který však roční výši kupónových plateb vztahuje nikoli k jmenovité hodnotě (jako v případě kupónového výnosu), nýbrž k aktuální tržní (čisté) ceně.

Na příkladu výše zmíněného modelového dluhopisu si můžeme ukázat výpočet běžného výnosu.

Běžný výnos je roven podílu roční kupónové platby (450 Kč) a čisté ceny dluhopisu (v prvním scénáři 9.900 Kč), což je po zaokrouhlení rovno 4,55 %.

Protože je v prvním scénáři tržní cena dluhopisu nižší než jeho jmenovitá hodnota, je tím pádem běžný výnos vyšší než kupónový.

Pokud by však tržní cena daného dluhopisu vzrostla, např. na 10.100 Kč jako v druhém scénáři, běžný výnos by se snížil. V našem druhém scénáři na přibližně 4,46 % (450/10.100).

Kupónový i běžný výnos jsou však jednoduššími, spíše orientačními způsoby, jak kvantifikovat výnos dluhopisu. Nezohledňují totiž časovou hodnotu peněz.

Výnos do splatnosti

Mezi nejsofistikovanější a nejvíce používané způsoby, jak stanovit výnos dluhopisu, se řadí výnos do splatnosti dluhopisu (YTM), který se dá charakterizovat jako úroková míra, při níž se současná hodnota veškerých budoucích příjmů plynoucích z držby dluhopisu rovná aktuální tržní ceně dluhopisu. Jinými slovy se jedná o aktuální průměrný roční výnos z dluhopisu (vztažený k jeho tržní ceně) od doby pořízení až po jeho splatnost, jenž bere v potaz výši kupónových plateb, rozdíl mezi aktuální tržní cenou a jmenovitou hodnotou a také počet let do splatnosti dluhopisu.

Vzorec pro výpočet výnosu do splatnosti u dluhopisu s frekvencí výplaty kupónu jednou ročně a tříletou splatností. P na levé straně rovnice značí aktuální tržní cenu, C jsou kupóny v jednotlivých letech vyplývající z držby dluhopisu. YTM se dá spočítat pomocí investiční kalkulačky či přes nástroj hledání řešení v MS Excel.

Příklad výpočtu YTM u dluhopisu s danými parametry pomocí MS Excel – pokud cena dluhopisu vzroste, výnos do splatnosti se při jinak nezměněných okolnostech sníží. Pokud je cena dluhopisu stejná jako jeho jmenovitá hodnota, YTM je roven roční kupónové sazbě (scénář 3):

Vztah mezi cenou a výnosem

Výnos do splatnosti a cena dluhopisu jsou navzájem v inverzním vztahu. Když cena roste, výnos klesá a naopak.

V případě, že je výnos do splatnosti nulový, je cena za dluhopis rovna součtu jednotlivých peněžních toků vyplývajících z držby dluhopisu. Naopak se stále rostoucím výnosem do splatnosti se cena dluhopisu blíží k nule.

Zdroj: B. Stádník: Teorie a praxe dluhopisů

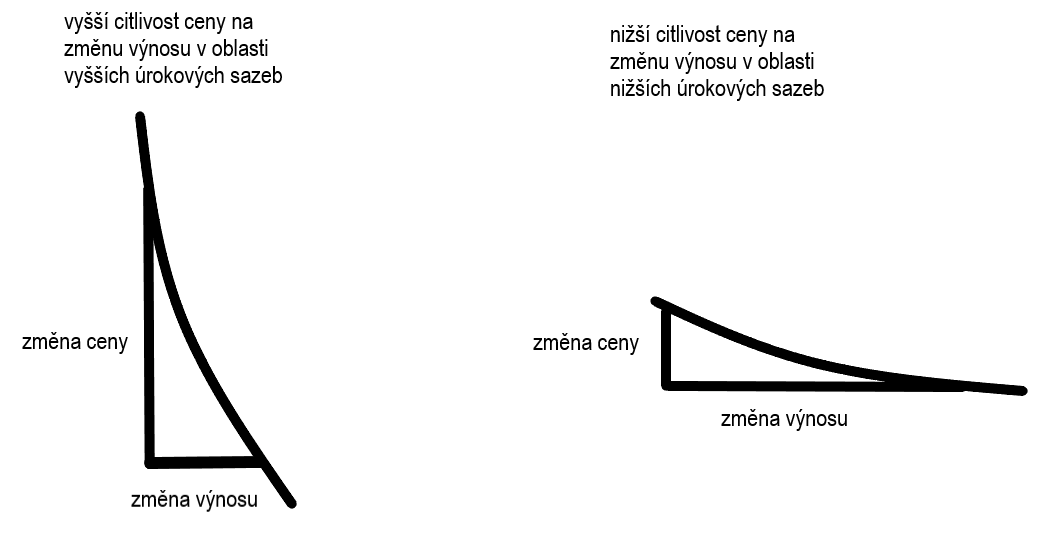
Z grafu je patrné, že citlivost ceny dluhopisu na změnu výnosu do splatnosti je vyšší v oblasti nižšího výnosu. Jinak řečeno, změna výnosu v oblasti nízkých úrokových sazeb vychýlí cenu dluhopisu více než stejná změna výnosu v oblasti vysokých úrokových sazeb, jak ukazují dva grafy níže, které vznikly přiblížením výše znázorněné křivky na obou jejích koncích.

Výše uvedený obrázek si můžeme představit na konkrétním příkladě. Pokud bude mít daný dluhopis výnos do splatnosti např. 5 % a tento výnos se v určitém okamžiku (z důvodu např. změny tržních úrokových sazeb) sníží na 2 % (= pokles o 3 procentní body), bude zvýšení ceny tohoto dluhopisu větší (graf vlevo) než kdyby jeho výnos do splatnosti poklesl z 15 % o 3 procentní body (graf vpravo).

Co je durace?

V článku jsme již uvedli, že dluhopisy s delší splatností mají vyšší citlivost ceny na změny úrokových sazeb. Pro zjištění, o kolik se změní cena dluhopisu či celého portfolia v reakci na změnu tržních úrokových sazeb používají analytici tzv. duraci.

Jedná se o průměrnou dobu splatnosti jednotlivých příjmů z dluhopisu. Čím je tato průměrná doba vyšší, tím vyšší je citlivost na změnu tržních úrokových sazeb. Závěrem tedy lze říci, že čím vyšší je durace, tím větší je také citlivost ceny na změnu tržních úrokových sazeb.

Na duraci mají vliv tři faktory. Jedním z nich je doba splatnosti, s jejíž délkou roste také durace. Dalšími dvěma faktory jsou výše kupónové sazby a výše tržních úrokových sazeb, které jsou s durací v inverzním vztahu – pokud tedy klesají, durace roste.

Durace bezkupónového dluhopisu je rovna zbývajícímu počtu let do splatnosti. S rostoucí kupónovou sazbou u dluhopisů stejných parametrů durace klesá, tudíž také citlivost na změnu úrokové sazby.

 

Přehled všech doposud vydaných dílů k dispozici zde.

 

Zdroje: B. Stádník: Teorie a praxe dluhopisů, J. Veselá: Investování na kapitálových trzích, P. Musílek: Trhy cenných papírů

 

Michal Fric
Fio banka, a.s.